| 立即下载 | 限时 免费 下载 |
同类热门下载
简介：
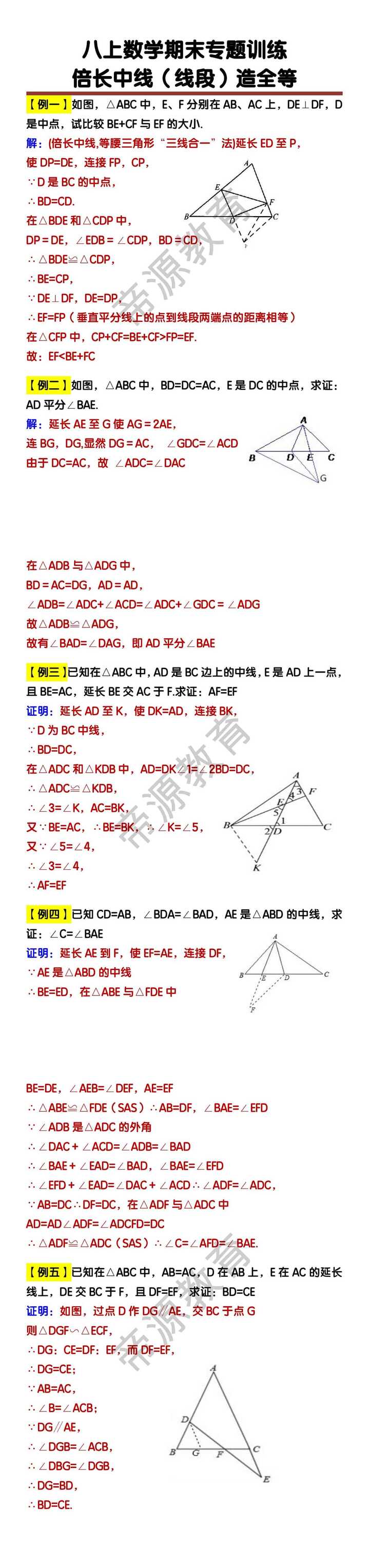
【例一】如图，△ABC中，E、F分别在AB、AC上，DE⊥DF，D是中点，试比较BE+CF与EF的大小.
解：(倍长中线,等腰三角形“三线合一”法)延长ED至P，
使DP=DE，连接FP，CP，
∵D是BC的中点，
∴BD=CD.
在△BDE和△CDP中，
DP＝DE，∠EDB＝∠CDP，BD＝CD，
∴△BDE≌△CDP，
∴BE=CP，
∵DE⊥DF，DE=DP，
∴EF=FP（垂直平分线上的点到线段两端点的距离相等）
在△CFP中，CP+CF=BE+CF>FP=EF.
故：EF<BE+FC
【例二】如图，△ABC中，BD=DC=AC，E是DC的中点，求证：AD平分∠BAE.
解：延长AE至G使AG＝2AE，
连BG，DG,显然DG＝AC， ∠GDC=∠ACD
由于DC=AC，故 ∠ADC=∠DAC
在△ADB与△ADG中，
BD＝AC=DG，AD＝AD，
∠ADB=∠ADC+∠ACD=∠ADC+∠GDC＝∠ADG
故△ADB≌△ADG，
故有∠BAD=∠DAG，即AD平分∠BAE
【例三】已知在△ABC中，AD是BC边上的中线，E是AD上一点，且BE=AC，延长BE交AC于F.求证：AF=EF
证明：延长AD至K，使DK=AD，连接BK，
∵D为BC中线，
∴BD=DC，
在△ADC和△KDB中，AD=DK∠1=∠2BD=DC，
∴△ADC≌△KDB，
∴∠3=∠K，AC=BK，
又∵BE=AC，∴BE=BK，∴∠K=∠5，
又∵∠5=∠4，
∴∠3=∠4，
∴AF=EF
浙ICP备13013615号-4